Welcome to the PDS Atmospheres Node

Standard Planetary Information, Formulae and Constants

Download a Postscript version created from LaTeX

Summary of constants
Tables of atmospheric parameters for the planets
Adiabatic Lapse Rate
Auto-convective Lapse Rate
Amagats
Beers Law
Beta plane approximation
Brunt Vaisala or Buoyancy Frequency
Cloud clearing eta and N* methods
Cloud properties
Dobson Units
Double Linear Interpolation
Earth: molecular abundances
Earth: Molecular spectral regions
Earth: Oceans
Equations of Motion
FFT, Cosine Transform
Gas Constant
Geopotential
Geostrophic Approximation
Gravity
Heat Balance
Humidity
Hurricanes
Hydrostatic Equilibrium
Ideal Gas Law
IR filter bandpasses
Latitude: planeto-graphic and planeto-centric
Longitude Systems and Conversion
Orbits: Equations of motion, Period(altitude)
Planck Function
Planet Mission Summary
Potential Temperature
Potential Vorticity
Radiative time constant
Radiative Transfer Equation (IR)
Rayleigh Scattering: Optical Depth
Rayleigh Scattering: Phase Function
Richardson Number
Rossby Number
Saturation Vapor Pressure
Scale Height
Thermal Wind Equation
Velocity of Sound
Vorticity
Weighting Functions
Wind Measurement

Physical Constants

(ref. Physics Today, Aug. 1995 pg. BG9)

AU = astronomical unit = 1.4960 · 10¹³ cm
c = speed of light = 2.99792458 · 10¹⁰ cm/s
G = 6.67259(85) · 10^-8 dyne cm²/gm²
h = Planck's constant = 6.626075(40) · 10^-27 erg sec
k = Boltzmann's constant = 1.380658(12) · 10^-16 erg/K
N_a = Avogadro's number = 6.0221367(36) · 10²³ gm/mole
sigma = Stefan-Boltzmann constant = 5.67051(19) · 10^-5 erg/s/cm²/K⁴
S₀ = 1.37 · 10⁶ erg/cm²
R_univ = N_a · k = 8.3143 · 10⁷ erg/mole/K
<mw>_H₂O = 18.016 gm/mole
<mw>_O₃ = 47.9982 gm/mole

Earth Constants

R_eq = 6378.388 km
M = 5.975 · 10²⁷ gm
<mw>_{dry air} = 28.964 gm/mole
R_g = 0.28705 · 10⁷ erg/gm/K
N₀ = Loschmidt's number = 2.686763(23) · 10¹⁹ molecules/cm³
g_s = Standard surface gravity = 980.665 cm/s
P_s = Standard surface pressure = 1.01325 · 10⁶ dyne/cm²
c_p = 1.006 · 10⁷ erg/gm/K at stp
c_v = 0.718 · 10⁷ erg/gm/K at stp
gamma = c_p/c_v = 1.401 at stp

Unit Conversion

1 knot = 1 nautical mile/hour = 1.151555 mile/hour = 1.853248 Km/hr
1 megaton = 4.2 · 10²² erg = 4.2 · 10¹⁵ Joule
1 AU = 1.495 · 10⁸ Km = 8.31 light minutes

Tables of atmospheric parameters for the planets

**Planet Size Information**
	area Km²	volume Km³	Mass grams	Mass M	density gm/cm³
Venus	4.6011e+08	9.2805e+11	4.8850e+27	0.817	5.264
Earth	5.1006e+08	1.0832e+12	5.9790e+27	1.000	5.520
Mars	1.4416e+08	1.6275e+11	6.4570e+26	0.108	3.967
Jupiter	6.1469e+10	1.4313e+15	1.8986e+30	317.551	1.327
Saturn	4.2694e+10	8.2713e+14	5.6854e+29	95.089	0.687
Uranus	8.0840e+09	6.8336e+13	8.6825e+28	14.522	1.271
Neptune	7.6280e+09	6.2637e+13	1.0310e+29	17.244	1.646
Titan	8.3323e+07	7.1519e+10	1.3500e+26	0.023	1.888

**Planet Rotation Period**
	hours	hr:mn:secs	day/earth	°/day
Venus	-5833.2000000	-5833:12: 0.0	-243.05000	1.481177
Earth	23.9333330	23:56: 0.0	0.99722	361.002791
Mars	24.6333330	24:38: 0.0	1.02639	350.744254
Jupiter: SI..	9.8416675	9:50:30.0	0.41007	877.900010
Jupiter: SII.	9.9279533	9:55:40.6	0.41366	870.270008
Jupiter: SIII	9.9249197	9:55:29.7	0.41354	870.536010
Saturn: SI..	10.2333290	10:14: 0.0	0.42639	844.300032
Saturn: SIII	10.6562220	10:39:22.4	0.44401	810.793919
Uranus	-17.2333330	-17:14: 0.0	-0.71806	501.353975
Neptune	16.1100000	16: 6:36.0	0.67125	536.312849
Titan	382.6799927	382:40:48.0	15.94500	22.577611

**Orbital Parameters**
	a(AU)	period(yrs)	inclin(°)	a.node(°)	arg.perih(°)	ecc	L(6430)(°)
Venus	0.7233	0.62	3.39	76.55	131.25	0.006818	267.689
Earth	1.0000	1.00	0.00	0.00	102.77	0.016704	99.372
Mars	1.5237	1.88	1.85	49.45	335.82	0.093329	195.082
Jupiter	5.2025	11.87	1.31	100.35	15.46	0.048075	329.233
Saturn	9.5531	29.53	2.49	113.55	92.20	0.051565	238.772
Uranus	19.2642	84.55	0.77	73.99	175.28	0.046227	253.217
Neptune	30.2337	166.24	1.77	131.82	7.60	0.007972	274.526
Titan	0.0082	0.04	0.33	0.00	0.00	0.030000	0.000

**Planet Pole**
	<r>(AU)	inclin(°)	RA(°)	DEC(°)
Venus	0.7233	177.40	272.78	67.21
Earth	1.0000	23.40	0.00	90.00
Mars	1.5237	25.20	317.57	57.52
Jupiter	5.2025	3.10	268.04	64.49
Saturn	9.5531	26.70	39.36	83.45
Uranus	19.2642	97.90	257.43	-15.10
Neptune	30.2337	29.00	295.33	40.65
Titan	0.0082	0.00	0.00	0.00

**Velocity**
	V_orbit Km/s	V_escape Km/s	V_equator Km/s	V_sound Km/s
Venus	35.022	10.378	-0.002	0.236
Earth	29.786	11.192	0.465	0.320
Mars	24.130	5.045	0.240	0.227
Jupiter	13.059	60.511	12.572	0.816
Saturn	9.637	36.376	9.871	0.716
Uranus	6.786	21.411	-2.589	0.543
Neptune	5.417	23.670	2.689	0.543
Titan	5.573	2.645	0.012	0.185

**Effective (T_eff,P_eff) Values**
	T_eff K	P_eff mBar	gm/cm³	H Km	V_sound m/s	_rad years	phase °
Venus	229.0	20.000	4.6230e-05	4.862	235.8	0.007	3.94
Earth	255.0	500.000	6.8297e-04	7.471	320.2	0.131	39.47
Mars	210.0	6.000	1.5124e-05	10.605	226.6	0.006	1.17
Jupiter	124.0	400.000	8.6132e-05	19.146	816.3	4.534	67.39
Saturn	95.0	300.000	8.1128e-05	36.975	715.5	20.794	77.27
Uranus	59.0	430.000	2.0161e-04	24.234	543.4	131.311	84.15
Neptune	59.0	500.000	2.3443e-04	19.206	543.4	121.008	77.67
Titan	85.0	1.000	4.0568e-06	18.152	184.7	0.053	82.54

**Stratopause Values**
	T K	P mBar	gm/cm³	H Km	V_sound m/s	_rad years	phase °
Venus	400.0	50.000	6.6166e-05	8.492	311.7	0.003	1.85
Earth	270.0	1.000	1.2901e-06	7.911	329.5	0.000	0.08
Mars	140.0	0.005	1.8905e-08	7.070	185.0	0.000	0.00
Jupiter	163.0	3.000	4.9143e-07	25.167	935.9	0.015	0.45
Saturn	145.0	2.000	3.5435e-07	56.435	884.0	0.039	0.48
Uranus	120.0	1.000	2.3053e-07	49.290	775.0	0.036	0.15
Neptune	130.0	2.000	4.2559e-07	42.319	806.7	0.045	0.10
Titan	170.0	1.000	2.0284e-06	36.304	261.3	0.007	43.69

**Tropopause Values**
	T K	P mBar	gm/cm³	H Km	V_sound m/s	_rad years	phase °
Venus	250.0	100.000	2.1173e-04	5.307	246.4	0.026	14.83
Earth	217.0	100.000	1.6051e-04	6.358	295.4	0.043	14.96
Mars	140.0	0.010	3.7809e-08	7.070	185.0	0.000	0.01
Jupiter	110.0	140.000	3.3983e-05	16.984	768.8	2.273	50.28
Saturn	85.0	100.000	3.0224e-05	33.083	676.8	9.677	64.10
Uranus	53.0	110.000	5.7414e-05	21.770	515.1	46.340	73.81
Neptune	54.0	200.000	1.0246e-04	17.579	519.9	63.132	67.26
Titan	70.0	100.000	4.9261e-04	14.949	167.7	9.506	89.96

**1 BAR Values**
	T K	P BAR	gm/cm³	H Km	V_sound m/s	_rad years	phase °
Venus	360.0	1.000	1.4704e-03	7.643	295.7	0.087	41.57
Earth	288.0	1.000	1.2094e-03	8.438	340.3	0.182	48.82
Mars	140.0	0.007	2.6466e-05	7.070	185.0	0.024	4.59
Jupiter	165.0	1.000	1.6182e-04	25.476	941.6	4.811	68.57
Saturn	134.0	1.000	1.9172e-04	52.154	849.8	24.699	79.23
Uranus	76.0	1.000	3.6399e-04	31.217	616.8	142.873	84.62
Neptune	76.0	1.000	3.6399e-04	24.740	616.8	113.230	76.85
Titan	86.0	1.000	4.0096e-03	18.66	185.8	51.265	89.99

**Surface (H₂O) Values**
	T K	P BAR	gm/cm³	H Km	V_sound m/s	_rad years	phase °
Venus	731.0	92.000	6.6619e-02	15.519	421.4	0.954	84.14
Earth	288.0	1.013	1.2252e-03	8.438	340.3	0.184	49.19
Mars	214.0	0.007	1.7314e-05	10.807	228.7	0.007	1.29
Jupiter	294.0	7.000	6.3574e-04	45.394	1256.9	5.953	72.40
Saturn	313.0	21.000	1.7237e-03	121.823	1298.8	40.698	83.41
Uranus	366.0	260.000	1.9651e-02	150.336	1353.5	332.598	87.68
Neptune	360.0	283.000	2.1746e-02	117.192	1342.3	301.495	84.98
Titan	94.0	1.500	5.5026e-03	20.074	194.3	58.887	89.99

Adiabatic Lapse Rate, Dry

from the first law of thermodynamics

dQ = dU +

W = n · c_v dT + P dV = 0
where c_v is given in units of erg/K/mole and n is the number of moles. The derivative of the ideal gas law, P · V = n R T, is

V dP + P dV = n R dT
equating P dV and noting that R = c_p - c_v yields

dQ = n c_v dT - V dP + n (c_p-c_v) dT

dQ = n c_p dT - V dP = 0 for adiabatic
C_p = c_p/<mw> and rho

= n · <mw>/V so that

dT/dP = V/(n · c_p) = 1 /(C_p · rho

)
From hydrostatic equilibrium and the gas law we can convert from pressure to height coordinates:

dP = - g

dT/dz|_a = -g/C_p

-dT/dz|_a = g/C_p

	<g> cm/s²	C_p J/gm/K	Adiabatic Lapse Rate K/Km	R_g J/gm/K	Autoconvective Lapse Rate K/Km
Venus	889.89	0.8501	10.468	0.18892	47.104
Earth	979.86	1.0040	9.760	0.28710	34.130
Mars	374.10	0.8312	4.500	0.18892	19.802
Jupiter	2425.61	12.3591	1.963	3.74518	6.477
Saturn	1000.09	14.0129	0.714	3.89246	2.569
Uranus	880.07	13.0137	0.676	3.61491	2.435
Neptune	1110.46	13.0137	0.853	3.61491	3.072
Titan	135.80	1.0440	1.301	0.29000	4.683

Autoconvective Lapse Rate

From hydrostatic equilibrium and the ideal gas law, P = R_g rho (z) T(z) we have

= -(1/g) · (dP/dz) = -(R_g/g) · [ T(z) d rho

/dz +

(z) dT/dz ]

dT/dz = - g/R_g - [T(z)/ rho

(z) · d

/dz]
But T(z) and rho

(z) are always positive so that when

-dT/dz

g/R_g
then d rho

/dz

0. Thus, the autoconvective criteria is that when the density increases with altitude the atmosphere will be forced to convectively adjust and this condition is met when

_auto

g/R_g

Amagats

From the ideal gas law we can define the number of particles at standard temperature (273.15 K) and standard pressure (1 atm = 1013.25 milli-bars). The ideal gas law can be written many ways, here we will adopt the notation(s)

P = N k T = rho

N_a k T/<mw> = rho

R_g T
where, N is the number of molecules per unit volume, Boltzmann's constant k = 1.3806 · 10^-16 erg/K, the gas constant
R_g = N_a · k/<mw>, Avogadro's number, N_a = 6.02 · 10²³ particles per mole, <mw> is the molecular weight in grams/mole.
This number of molecules at STP is called Loschmidt's number and has the value,

N₀ = P_stp/(k · T_stp) = 2.687 · 10¹⁹ cm^-3
The number of amagats of a gas is given as a ratio of the actual number of particles at the given temperature and pressure to Loschmidt's number. In planetary atmospheres the number density is a function of height. We can calculate the thickness of an equivalent atmospheric column at standard temperature and pressure. This is denoted as cm-amagats or Km-amagats and is given by

Z = (1/N₀) integ

N_i(z) · dz
Hydrostatic equilibrium relates the pressure and vertical coordinates

g dz, or dz = -dP/( rho

g),
and the number density, N_i can be written as a function of the density,

N_i = q_i · rho

N_a/<mw>, molecules/cm³
where, q_i is the volumetric fraction of species i.

Z = N_a/(g N₀) integ

q_i/<mw> · dP approx

N_a/(g N₀) · ( q_i/<mw>) · P = H₀ · P

H₀ = 10 · N_a q_i/(g N₀ <mw>) Km-amagat/Bar

	Earth	Mars	Jupiter	Saturn	Titan	Uranus	Neptune
g	981.0	374.1	2425.3	1000.0	136.0	880.1	1110.5 cm/s
q(H₂)	1.00	1.00	0.90	0.96	1.00	0.85	0.85
<mw>	28.97	44.01	2.22	2.14	28.00	2.30	2.30 gm/mole
H₀	7.88	13.61	37.45	100.50	58.85	94.08	74.56 Km-am/Bar
1000/H₀	126.9	73.49	26.70	9.95	16.99	10.63	13.41 mB/Km-am

Beer's Law

^u = e^{-sec() dz}

(CO₂,CO,CH₄,N₂O) + kappa

(H₂O) +

(O₃)

Transmittance between the top of the atmosphere and level at z is a function of the quantity and absorption of all gases.

The taller the glass, the darker the brew,

The less the amount of light that comes through.

Beta Plane Approximation

f = 2 ·

· sin(

)

f₀ + f' ·

= f' = (2 · Omega

· cos(

))/R(

) =

₀ · (R_eq/R( phi

)) · cos(

₀

/R_eq

	rad/s	f(45) s^-1	f(60) s^-1	f/f_earth	₀ (cm*s)^-1
Venus	-2.9921e-07	-4.2314e-07	-4.2314e-07	-0.004103	-9.889e-16
Earth	7.2925e-05	1.0313e-04	1.0313e-04	1.000000	2.287e-13
Mars	7.0852e-05	1.0020e-04	1.0020e-04	0.971583	4.176e-13
Jupiter	1.7585e-04	2.4869e-04	2.4869e-04	2.411438	4.920e-14
Saturn	1.6378e-04	2.3163e-04	2.3163e-04	2.245949	5.435e-14
Uranus	-1.0128e-04	-1.4323e-04	-1.4323e-04	-1.388781	-7.925e-14
Neptune	1.0834e-04	1.5321e-04	1.5321e-04	1.485620	8.730e-14
Titan	4.5608e-06	6.4500e-06	6.4500e-06	0.062541	3.542e-14

Brunt Vaisala or Buoyancy Frequency

N² = (R_g/H(z)) · [ dT₀/dz + (R_g/C_p) · (T₀(z)/H(z)) ] = (R_g/H(z)) · [ dT₀/dz + g/C_p ] = (R_g/H(z)) · sigma

where, T₀(z) = <T(z, phi

,t)>, i.e., temperature averaged over longitude lambda

, latitude phi

, and time t.
The static stability, sigma

, is related to the buoyancy frequency as

dT₀/dz + g/C_p
The static stability is positive for stable conditions and zero or negative for unstable conditions.

Cloud clearing, 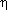method

Given the clear radiance, R_clr and the fraction of clouds, alpha _i in scene i.

R_i = (1- alpha

_i) · R_clr + alpha

_i · R_cld

R_clr = R₁ + eta

· ( R₁ - R₂ )

₁/(

₂ -

₁)

Chahine, M.T. 1974, J. Atmos. Sci. 31 p.233

Susskind, J., J. Joiner and C.D. Barnet 1995. Determination of atmospheric and surface parameters from simulated AIRS/AMSU sounding data. I. Retrieval methodology. submitted to J. Atmos. Oceanic Tech. (JAOT) Sep. 1995.

Cloud clearing, N^* method

N^*

₁/

₂ = (R₁ - R_clr)/(R₂ - R_clr)

R_clr = (R₁ - N^* R₂)/(1 - N^*)

= N^* / (1 - N^*)

McMillin, L.M. and C. Dean 1982. Evaluation of a new operational technique for producing clear radiances. J. Appl. Meteor. 21 p.1005-1014.

Smith, W.L. 1968. An improved method for calculating tropospheric temperature and moisture from satellite radiometer measurements. Monthly Weather Review 96 p.387-396.

Clouds, Properties

from NOAA chart

low clouds:

up to 6500 ft

up to 2 Km

up to 800 mBar (275 K)

Sc,St,Cu,Cb (Stratocumulus,Stratus,Cumulus,Cumulonimbus)

middle clouds:

6500 ft to 23,000 ft

2 Km to 7 Km

800 mBar to 400 mBar (240 K)

Ac,As,Ns (Altocumulus, Altostratus, Nimbostratus)

high clouds:

16,500 to 45,000 ft

5 Km to 13.75 Km

530 mBar (255 K) to 140 mBar (216 K)

Ci,Cc,Cs (Cirrus, Cirrocumulus, Cirrostratus)

	R_eff	V_eff (Hansen, 1971)
Fair Weather cumulus	5.56	0.111
Altostratus	7.01	0.113
Stratus	11.19	0.193
Cumulus congestus	10.48	0.147
Stratocumulus	5.33	0.118
Nimbostratus	10.81	0.143

Earth is typically covered about 50%
average precipitable water is about 2.5 cm
average time aloft is 9 days (from 100 cm of rain/year)
in thunderstorm approximately 10% of water is released

suspended droplets 1 µm to 100 µm
cloud over continents have smaller droplets

Dobson Units

DOBSON

10^-3 cm-amagat
given the number density, N, in molecules per cm³ then

_x = (<mw>_x · N_x(z))/N_a grams/cm²

C(L)

N(z) dz

<N(L)> ·

z = <N(i)> · Delta

P/(

_t g) = q · N_a · Delta

P/(<mw> g) molecules/cm²
Note that rho

= q ·

_t = N · <mw> /N_a where q is the volumetric mixing ratio of the species being measured.
To convert to mass column density, M, in grams per cm²

M(L) = (<mw>_O₃ /N_a) · C(L) = Delta

P/ g

DOBSON = 1000 * Z = 1000 * sum

C(L) / N₀
where N₀ is Loschmidt's number.

The atmosphere consists of fixed gases (e.g., CO₂, N₂O, CO), water, and ozone so the pressure within any level is given as

p(L)

_t g dz = g integ

(

_f +

_w +

_o) dz
so that

p(L) · N_a / g = <mw>_f · C_f(L) + <mw>_w · C_w(L) + <mw>_o · C_o(L)

C_f(L) = ( Delta

p(L) · N_a)/(<mw>_f · g) - (<mw>_w/<mw>_f) · C_w(L) - (<mw>_o/<mw>_f) · C_o(L)
we can also define the total column density as

C_t(L)

(

p(L) · N_a) / (<mw>(L) · g)
and if we require

C_t(L) = C_f(L) + C_w(L) + C_o(L)
then,

<mw>(L) = (<mw>_f · C_f(L) + <mw>_w · C_w(L) + <mw>_o · C_o(L)) / C_t(L)
C_t(L) in eqn 6 and <mw> can be solved for iteratively with an initial guess of <mw> = <mw>_f
The volumetric mixing ratio, i.e., molecules of species x to the total number of molecules, is given by

f_o(L) = C_o(L) / C_t(L) = C_o(L) / ( Delta

P(L) · N_a) · <mw>(L) · g

Double Linear Interpolation

Delta x = s - s₀, 0 leq Delta x leq 1
Delta y = l - l₀, 0 leq Delta y leq 1
s₁ = s₀ + 1, l₁ = l₀ + 1
DN(s,l₀) = DN(s₀,l₀) + Delta x · (DN(s₁,l₀)-DN(s₀,l₀))
DN(s,l₁) = DN(s₀,l₁) + Delta x · (DN(s₁,l₁)-DN(s₀,l₁))
DN(s,l) = DN(s,l₀) + Delta y · (DN(s,l₁) - DN(s,l₀))
or
DN(s,l) = DN(s₀,l₀)

x · (DN(s₁,l₀)-DN(s₀,l₀))

y · (DN(s₀,l₁)-DN(s₀,l₀))

y · (DN(s₁,l₁) + DN(s₀,l₀) - DN(s₀,l₁) - DN(s₁,l₀))

Earth: molecular abundances

From US Standard Atmosphere 1976, Table 3 and page 33 (Trace Constituents)

Gas	<mw> gm/mole
H	1.00794
C	12.011
N	14.00674
O	15.9994
S	32.066

Gas	<mw> gm/mole	volumetric f_i
N₂	28.0134	0.78084
O₂	31.9988	0.209476
Ar	39.948	0.00934
CO₂	44.00995	314 ppmv
Ne	20.183	18.18 ppmv
He	4.0026	5.24 ppmv
Kr	83.80	1.14 ppmv
Xe	131.30	0.087 ppmv
CH₄	16.04303	1.5 ppmv
H₂	2.01594	0.5 ppmv
<<mw>>	28.9644
H₂O	18.016	f 0.005 at 1 km (900 mB)
O₃	47.9982	f 20 ppmv at 36 km (5 mB)
N₂O	44.0129	270 ppbv
NO	30.0061	0.5 ppbv
NO₂	46.0055	1 ppbv
H₂S	34.0819	0.05 ppbv
NH₃	17.0306	4 ppbv
SO₂	64.0648	1 ppbv
CO	28.0104	190 ppbv

Methane, CH₄
1992 1.7086 ppm
1984 1.6180 ppm --> +0.0113 ppm/year = +0.7 %/year
0.02 ppm peak-to-peak seasonal variation = ± 0.01 ppm = ± 0.62 %
q_CH₄ = 1.618 + 0.0113 · (t-1984.0) ± 0.01 ppm

Carbon Dioxide, CO₂
1995 361.0 ppm
1980 336.8 ppm --> +1.6 ppm/year = +0.475 %/year
0.105 ppm peak-to-peak seasonal variation = ± 0.052 ppm = ± 0.015 %
q_CO₂ = 337 + 1.6 · (t-1980.0) ± 0.052 ppm

C¹²O¹⁶O¹⁸ = 4.08 · 10^-3 · C¹²O¹⁶O¹⁶
C¹²O¹⁶O¹⁷ = 7.42 · 10^-4 · C¹²O¹⁶O¹⁶ Kiehl & Ramanathan 1983. JGR 88 p.5191.
C¹³O¹⁶O¹⁶ = 1.12 · 10^-2 · C¹²O¹⁶O¹⁶

Earth: molecular spectral regions

CO₂ 15 µm spectral region
₂ (667.381 bending mode) vibrational-rotational band
₁ (1388.23 symmetric stretch mode) fermi-resonance stimulated by ₂ (618.029, 720.805)
B(CO₂) = 0.39 cm^-1
Q-branch at 667.5 (2 mb)
line wings have 1.5 scale height wide weighting functions
line centers have 2.5 scale height weighting functions

**CO₂ band correlation parameters at 180 K, Cess & Ramanathan, 1972**
band cm^-1	S at 180 K cm^-2 amagat	A₀ cm^-1	₀ atm^-1 cm^-1	d cm^-1
667	549	17.3	0.097(300/T)^(2/3)	1.56
2350	4505	15.4	0.097(300/T)^(2/3)	??
3715	102	32.2	0.097(300/T)^(2/3)	??

**CO₂ band correlation parameters, Kiehl & Ramanathan, 1983**
band cm^-1	transition ₁₂₃	S at 300 K cm^-2 amagat	E_j cm^-1	d cm^-1
667.381	00⁰0 --> 01¹0	194	0.0	1.56
667.751	01¹0 --> 02²0	15	667.381	0.78
720.805	(I) 01¹0 --> 10⁰0	5.00	667.381	1.56
618.029	(II) 01¹0 --> 10⁰0	4.27	667.381	1.56
668.107	02²0 --> 03³0	0.85	1335.131	0.78
647.063	(II) 10⁰0 --> 11¹0	0.7	1285.410	1.56
668.670	(I) 10⁰0 --> 11¹0	0.3	1388.185	1.56

NOTE: for C¹²O¹⁶O¹⁷ and C¹²O¹⁶O¹⁸ the mean line spacing is 0.78 for all bands

₀ = 0.067 (300/T)^(2/3) atm^-1 cm^-1

A₀ = 22.18 (T/296)^0.5 cm^-1

S(T)

S(T₀) · (T₀/T) [ (1 - exp(-1.439

/T))³ ] / [(1 - exp(-1.439

/T₀))³ ]

CO₂ 4.3 µm spectral region
₃ (2349.16 asymmetric stretch mode) band, no Q-branch
high T dependence of high J lines makes narrower weighting functions free of isotopes and hot lines

H₂O 6.3 µm spectral region}

band	H₂O	HDO
₁	3657.05	2723.68
₂	1594.75	1403.49
₃	3755.93	3707.47

non-linear molecule with angle of 104.45° ₁ ~ ₃ ~ 2 · ₂

O₃ 9.6 µm spectral region
₁ 1110 cm^-1
₂ 1045 cm^-1
₃ 701 cm^-1

CH₄ spectrum
of the 9 modes, only ₁ through ₄ are independent, and ₃ and ₄ are triply degenerate.
¹³C is 1.108 % of all Carbon

**The Strongest Bands of Methane (rel. to ground state) from Andrews et al.**
band	¹²CH₄	¹³CH₄
₄	1310.76	1302.77
₂	1533.37
₃	3018.92	3009.53
2₄	2612
₂ + ₄	2830	2822
2₂ + ₄	3062
₁ + ₄	4223
₃ + ₄	4340
₂ + ₃	4540

**CH₄ band correlation parameters, Cess & Chen, 1975**
band cm^-1	S cm^-2 amagat^-1	A₀ cm^-1	₀ atm^-1 cm^-1	d cm^-1
1306	185	52(T/300)^0.5	0.075(300/T)^0.5	5.3
3020	320	124(T/300)^0.5	0.075(300/T)^0.5	10.5
4220	20	124(T/300)^0.5	0.075(300/T)^0.5	10.5
5861	3	124(T/300)^0.5	0.075(300/T)^0.5	10.5

Earth: Oceans

Thermocline:

ocean layer in which temperature decreases rapidly with depth. From 200 to 1000 meters the temperature decreases by 15 degrees F. In summer the thermocline becomes thin and gradients of 1 degree per foot can be observed.

Oceans:

P = g*

P(Bar) = 981 cm/s² * 12*2.54 * Z(ft) * rho (gm/cm³) * 1.0E-6 Bar/(dyn/cm²)
P(Bar) = 31.0 * Z(1000 ft)

Z(ft)	(gm/cm³)
0	1.028 (assume 35 parts-per-thousand salinity)
1000	1.033
2000	1.0375
20000	1.071

Z	P
320	10 Bar
3,200	100 Bar
3,790	120 Bar <Z> of all Oceans - depth of life Zone
4,690	145 Bar depth of Mediterranean
4,900	150 Bar maximum depth of life
7,282	225 Bar depth of Gulf of Mexico
20,000	600 Bar max. depth of Atlantic
35,600	1100 Bar 1960 depth of Trieste into Chall.II (7 miles!!)

Note: ratio of Volume of Ocean to Land (above Z=0) = 11
ratio of Area of Ocean to Land:

N 61:39 = 3:2

S 81:19 = 4:1

all 142:58 = 5:2
source: 1982 Encyclopedia Brittanica

Equations of motion

Momentum

dV/dt = - 2 Omega

· V - (1/ rho

)

P + k g + F

i u + j v + k w

du/dt - 2

v sin(

) = (-1/ rho

) ( P/ x) + (u v tan( phi

)/a) - (u w/a) - 2 Omega

w cos(

) + F_x

dv/dt + 2

u sin(

) = (-1/ rho

) ( P/ y) - (u² tan( phi

)/a) - (v w/a) + F_y

dw/dt - 2

u cos(

) = (-1/ rho

) ( P/ z) + ((u² + v²)/a) - g + F_z

Continuity

(1/

) (d

/dt) + · V = 0
when motions are on the order of a scale height or less

· (

₀V) = 0

Energy

q'/T = c_p (d log_e( Theta

)/dt) = (c_p/T) (dT/dt) - (R_univ/P) (dP/dt)

FFT

Forward FFT

F(u) = FFT(f(x),-1) ident

1/m

f(x) · e^{-i · u · (2 x/m)} for u = 0,m-1

Inverse FFT

f(x) = FFT(F(u),+1) ident

F(u) · e^{i · x · (2 u/m)} for x = 0,m-1

Forward Cosine transform

F(u)

(1/m) ·

f(x) · cos(u ·

x/m) · dx

[(f(0) + f(m) · cos(

u))/2 m] + 1/m sum

f(x) · cos(u ·

x/m) = FFT(g(x),-1)

g(x) = f(x) for x = 0,m

g(2m-x) = f(x) for x = 1,m-1

Inverse Cosine Transform

f(x) = F(0) + F(m) · cos(

x) + 2 · sum

F(u) · cos(x ·

u/m) = FFT(G(u),+1)

G(x) = F(x) for x = 0,m

G(2m-x) = F(x) for x = 1,m-1

Gas Constant

R_univ = c_p - c_v = 8.3143 Joules/mole/K = 8.3143 · 10⁷ erg/mole/K

<mw>_air = 28.964 gm/mole

R_g(air) = R_univ/<mw>_air = 287.05 Joule/Kg/K

C_p(air) = 1005 J/Kg/K

R_g/C_p = R_univ/c_p

C_p/C_v = c_p/c_v

	<mw> gm/mole	R_gas J/gm/K	C_p J/gm/K
Venus	44.01	0.18892	0.8501	0.2222	1.2857
Earth	28.96	0.28710	1.0040	0.2860	1.4005
Mars	44.01	0.18892	0.8312	0.2273	1.2941
Jupiter	2.22	3.74518	12.3591	0.3030	1.4348
Saturn	2.14	3.89246	14.0129	0.2778	1.3846
Uranus	2.30	3.61491	13.0137	0.2778	1.3846
Neptune	2.30	3.61491	13.0137	0.2778	1.3846
Titan	28.67	0.29000	1.0440	0.2778	1.3846

Geopotential

= -g · dz

Geostrophic Approximation

Horizontal motions are in balance with the pressure gradient force. Friction is negligible ( i.e., far away from surface). Steady flow with small curvature ( i.e., dV/dt = 0 ). Works well for z geq 1 km, phi > 10°.

· f · V_g = P/ x

· f · U_g = P/ y

Gravity

**Gravitational Forces**
	<g> cm/s²	<g> g_earth	g(0) cm/s²	g(45) cm/s²	g(90) cm/s²
Venus	889.89	0.9082	889.89	889.89	889.89
Earth	979.86	1.0000	976.81	981.29	987.16
Mars	374.10	0.3818	372.40	374.90	378.10
Jupiter	2425.61	2.4755	2256.64	2504.58	2833.44
Saturn	1000.09	1.0206	882.36	1055.28	1283.11
Uranus	880.07	0.8982	860.29	889.23	928.60
Neptune	1110.46	1.1333	1087.16	1121.31	1167.07
Titan	135.80	0.1386	135.80	135.80	135.80

q = (

² · a³)/(G · M)

	10⁶*J2	10⁶*J4	10⁶*J6	10⁶*q
Venus
Earth
Mars	1960.454
Jupiter	14697	-584.0	31.0	89180
Saturn	16331	-914.0	108.0	154766
Uranus	3516	-31.9	0.0	29513
Neptune	4000	0.0	0.0	28960
Titan

Hubbard and Marley (1989)
Kieffer

Heat Balance

F_sun = S₀/<r_s>² S₀ ident

1.37 · 10⁶ ergs/cm²

P_abs = (1 - A_b) · F_sun · sunlit area = (1 - A_b) · F_sun ·

· R_eq · R_pl

a = total area = 2

· R²_eq +

(R²_pl/e) · log_e [ (1 + e)/(1 - e)]

e =

[R²_eq-R²_pl]/R_eq

F_abs = P_abs/a

T_eq = [P_abs/(a · sigma

)]^0.25
If the eccentricity is equal to zero, e = 0, then

a = 4

· R_eq · R_eq

F_abs = (1 - A_b) · F_sun/4

T_eq = [ (1 - A_b) · F_sun/(4 · sigma

) ]^0.25

	bond albedo	F_sun erg/s/cm²	F_abs erg/s/cm²	P_abs erg/s	T_eq K
Venus	0.750	2618462.8	163653.9	7.5299e+23	231.89
Earth	0.306	1370000.0	237414.7	1.2110e+24	254.49
Mars	0.250	590102.3	110447.6	1.5922e+23	210.18
Jupiter	0.343	50616.0	8123.3	4.9933e+24	109.45
Saturn	0.342	15011.7	2381.4	1.0167e+24	80.54
Uranus	0.300	3691.7	641.0	5.1818e+22	58.01
Neptune	0.290	1498.8	264.0	2.0141e+22	46.47
Titan	0.220	15011.7	2927.3	2.4391e+21	84.80

P_int = F_int · a

F_out = F_int + F_abs

ratio = F_out/F_abs = (F_int + F_abs)/F_abs

T_eff = (F_out/ sigma

)^0.25

	F_int erg/s/cm²	P_int erg/s	F_abs+F_int erg/s/cm²	T_eff K	out/in ratio
Venus	0.0	0.0000e+00	163653.9	231.89	1.0000
Earth	62.0	3.1624e+20	237476.7	254.51	1.0003
Mars	0.0	0.0000e+00	110447.6	210.18	1.0000
Jupiter	5440.0	3.3439e+24	13563.3	124.42	1.6697
Saturn	2010.0	8.5815e+23	4391.4	93.85	1.8440
Uranus	42.0	3.3953e+21	683.0	58.94	1.0655
Neptune	433.0	3.3029e+22	697.0	59.24	2.6399
Titan	0.0	0.0000e+00	2927.3	84.80	1.0000

Humidity

Absolute humidity

From the ideal gas law, the density of water, rho

_w is given by

_w= ( <mw>_w f_w e)/(R_* T)
where <mw>_w is the molecular weight of water (18.016 gm/mole), f_w is a correction factor for non-ideal behavior which can be taken as f_w = 1, e is the partial pressure of water, R_* is the universal gas constant, and T is the local temperature.

Specific humidity

The total density, rho

, is given by the sum of dry and moist densities ( i.e., assumes all other species are included in ``dry'').

_d +

_w = [ <mw>_d · (P - f_w e)]/(R_* T) + (<mw>_w f_w e)/(R_* T) = [<mw>_d · (P - 0.37803 f_w e)]/(R_* T)
where <mw>_d is the molecular weight of dry air (28.966), <mw>_w/<mw>_d = 0.62197, and (<mw>_d - <mw>_w)/<mw>_d = 0.37803. The specific humidity is the ratio of the moist to total density and is dimensionless, but is usually expressed in gm/Kg units.

q =

_w/

= (0.62197 f_w e) / (P - 0.37803 f_w e) appeq

0.622 e/P
Note that

_w = q ·

and the volumetric mixing ratio, f, (i.e., ratio of water number density, N_w, to the total number density N_t) is given by

f_w

N_w/N_t = <mw>/<mw>_w · q
where the average molecular weight, <mw>, is given by

<mw> = <mw>_d · (1 - f_w) + <mw>_w · f_w

Mass Mixing Ratio

r =

_w/

_d = 0.62197 · [(f_w e)/(P - f_w e)] appeq

0.62197 · e/(P - e) approx

from US Standard Atmosphere 1976, Table 20, pg. 44, r(z) ppm by mass
Alt (km)	P (mB)	record low	1% low	midlat. mean	1% high	record high
sfc	1013.25	0.1	5.0	4,686	30,000	35,000
1	890	24.0	27.0	3,700	29,000	31,000
2	790	21.0	31.0	2,843	24,000	28,000
4	610	16.0	24.0	1,268	18,000	22,000
6	470	6.2	12.0	554	7,700	8,900
8	350	6.1	6.1	216	4,300	4,700
10	265		5.3	43.2	1,300
12	195		1.2	11.3	230
14	140		1.5	3.3	48
16	100		1.0	3.3	38

% Relative Humidity

100 · r/r_s appeq

100 q/q_s appeq

100 e/e_s
where r_s ident

r(e = e_s) and q_s ident

q(e = e_s).
The saturated vapor pressure is approximately given by

e_s

6.11 · 10^{[(a T)/(b + T)]} mBar

r_s

0.62197 · e_s/(P - e_s) for e_s > P

r_s

0.62197 for e_s geq

P
where T is given in °C and a and b are constants.

	a	b
above water	7.5	237.3
above ice	9.5	265.5

Dew Point Temperature

The Dew point is the temperature at which the partial pressure of water reaches the saturation value, that is

e = (

_w R_* T)/(<mw>_w f_w) = e_s(T_dp)
The empirical expression for e_s can be used or a table lookup can be utilized after e is calculated.

Hurricanes

**Tropical Classification**
Gale force winds	(> 15 m/s)
Tropical Depression	(20-34kts and a closed circulation)
Tropical Storm (named)	(35-64kts)
Hurricane	(65+kts or 74+mph)

**Saffir-Simpson Scale**
	knots	m/h	Ps,(mB)	inch.Hg
Category 1	64- 83	74- 95	>980	>28.94
Category 2	83- 95	96-110	965-979	28.50-28.91
Category 3	96-113	111-130	945-964	27.91-28.47
Category 4	114-135	131-155	920-944	27.17-27.88
Category 5	>135	>155	<920	<27.16

Note: 1 knot = 1 nautical mile/hour = 1.151555 mile/hour = 1.853248 Km/hr

Storm	Date	Cat	Pc	Rc	winds
Nancy	Sep.12,1961		888		185 kt
Tip	Oct.12,1979		870		85 m/s
Camille	1969	5	909		165 kt
Allen	1980				165 kt
Gilbert	Sep. 1988		888
Hugo	1989	4
Andrew	1992	4	922

Empirical formula for approximate energy, ergs, of a storm with a central pressure, P_c, given in mBar and a radius of nearest circular isobar, R_c, given in kilometers is

E = 0.712 · 10²² · (1010 - P_c) · (R_c/111)² ergs

Hydrostatic Equilibrium

-g ·

· dz = -g · n · <mw>/V · dz
If the Ideal gas law holds (note: R_g = R_univ/<mw>), then

P = -P · (g · <mw>)/ (R_univ T) · dz = -P · dz/H(z), where H(z) = R_g(z) · T(z)/g(z)
If the scale height is constant, then

P = P₀ · exp(-z/H₀), where H₀ = R_g · T/g

Ideal Gas Law

P · V = N · k · T = n · R · T
where N is the total number of molecules, n is the total number of moles, N_a = 6.02217 · 10²³ molecules/mole, R_univ = 8.314 · 10⁷ erg/K/mole, k = R_univ/N_a = 1.380622 · 10^-16 erg/K

P = (N/V) k T = ( rho

· N_a/<mw>) k T

R_g

R_univ/<mw> erg/K/gm

P =

· (R_univ/<mw>) · T = rho

R_g T

IR filter bandpasses

	µm	range	trans	thick
J	1.25	1.1 - 1.4	60%	2.0mm
H	1.65	1.5 - 1.8	60%	2.0mm
K	2.20	2.0 - 2.4	60%	1.5mm
L	3.82	3.5 - 4.15	60%	1.0mm
M	4.70	4.4 - 5.0	60%	1.0mm

Latitude: planeto-graphic and planeto-centric

Planeto-centric latitude, theta and the planeto-graphic latitude, phi

R_eq/R_pl

= tan^-1 [ tan( phi

² ]

= tan^-1 [ tan( theta

) ·

² ]

) = R_eq R_pl/ sqrt

[R²_eq · sin²( theta

) + R²_pl · cos²( theta

)]

f = (R_eq - R_pl)/R_eq

e =

[ R²_eq - R²_pl]/R_eq = sqrt

[ 1 - (R_pl/R_eq)²]

S = total area = 2

· R²_eq +

(R²_pl/e) · log_e [ (1 + e)/(1 - e) ]

V = total volume = 4/3

R²_eq · Rpl
If e = 0 then

S = 4

· R_eq · R_eq

CRC Standard Mathematical Tables 26th edition, pg. 129. The volume of an oblate sphere is equal to a sphere with radius <R>.

<R> = (R²_eq · R_pl)^(1/3)

	R_eq Km	R_pl Km	R_eq/R_pl	f	e	<R> Km
Venus	6051.0	6051.0	1.000000	0.000000	0.000000	6051.00
Earth	6378.5	6356.0	1.003540	0.003527	0.083920	6370.99
Mars	3393.0	3375.0	1.005333	0.005305	0.102869	3386.99
Jupiter	71492.0	66854.0	1.069375	0.064874	0.354316	69911.33
Saturn	60268.0	54364.0	1.108601	0.097962	0.431658	58232.01
Uranus	25559.0	24973.0	1.023465	0.022927	0.212906	25362.16
Neptune	24820.0	24274.0	1.022493	0.021998	0.208597	24636.66
Titan	2575.0	2575.0	1.000000	0.000000	0.000000	2575.00

Longitude Systems and conversion

P₁ = reference rotational period of system #1
P₂ = reference rotational period of system #2
L₁(t-t₀) is a known system #1 longitude relative to time t₀
L₂(t-t₀) is the desired longitude value in system #2 relative to time t₀

L₂(t-t₀) = L₁(t-t₀) + L₂₁ + (t-t₀) · [ (24 · 360/P₂) - (24 · 360/P₁) ]
L₂₁ is a reference longitude. It is defined as:

L₂₁= L₂(t=t₀) - L₁(t=t₀)

Jupiter

S_I = 9h 50m 30.003s = 877.90°/24h. Used for equatorial motions.
S_II = 9h 55m 40.632s = 870.27°/24h. Used for mid-latitudes and GRS.
S_III = 9h 55m 29.711s ± 0.04s = 9.9249197h ± 0.000011h = 870.536°/24h ± 0.000966°/24h

_I = 67.10 + 877.900 · (t-t₀)

_II = 43.30 + 870.270 · (t-t₀)

_III = 284.95 + 870.536 · (t-t₀)

(S_III) =

(S_I) + 217.85 - 7.364 · (t-t₀)

(S_III) =

(S_II) + 241.65 - 0.266 · (t-t₀)
where t₀ = 2451545.0 TDB or Jan. 1.5, 2000.

U_III(S_I) = 106.35 m/s

U_III(S_II) = -3.4 m/s

Saturn

S_III = 10h 39m 22.4s ± 7s = 10.656222h ± 0.00194h = 810.7939024°/24h ± 0.148°/24h

_III = 38.90 + 810.793902 · (t-t₀)

_I = 227.2037 + 844.3 · (t-t₀)

(S_III) =

(S_I) + 171.6963 - 33.5061 · (t-t₀)

U_III(S_I) = 410.36 m/s

For the Voyager encounters the reference time should be set to the closest approach time. Other possibilities are:

	P₁	P₂	FDS(t=0)	L₂₁
Neptune	17.866	16.11	11200.0	-334.5365

Orbital: Equations of Motion

<r> = a/[ 1 + (e²/2) ]

Orbits: Earth

V =

t[ (G · M)/r ] cm/sec
where,

G = 6.67 · 10^-8 dyne cm²/gm²

M = 5.975 · 10²⁷ grams

r = 10⁵ · (<R> + z)

R = 6374.87 Km

P = (2 ·

· r)/(V · 3600) hours

V_g = (2 ·

· 10⁵ · R)/(P · 3600) cm/sec

r(Km)	P(hr)	V(Km/s)	V_g(Km/s)
200.0	1.474	7.786	7.549
400.0	1.542	7.670	7.217
700.0	1.645	7.505	6.763
900.0	1.715	7.401	6.486
35863.9	24.000	3.072	0.464

Planck function

The Planck function, B(T), is given by

B(T) = (

₁

³)/[exp(

₂

/T) - 1]
where,

= wavenumber in cm^-1 = 10⁴/ lambda

in µm.

T = temperature in degrees Kelvin

₁ = 2 h c² = 1.191066 · 10^-5 for radiance in units of mW · m^-2 · steradian^-1/cm^-1.

₂ = h c / k = 1.438833 K/cm^-1

h is Planck's constant (6.62620 · 10^-34 Joule)

c is the speed of light (2.99793 · 10⁸ m/second)

k is Boltzmann's constant (1.38062 · 10^-23 Joule/K)

is the Stefan-Boltzmann constant = 5.67 · 10^-5 erg · s^-1 · cm^-2 · K^-4 or mW · m^-2 · K^-4

Radiant Energy = A · sigma

· T⁴

The brightness temperature, T_b, of a given radiance, R, is found with the inverse of the Planck function.

T_b

B^-1

) = (

₂ ·

)/ log_e [ 1 + ( alpha

₁

³/R

) ]

The derivative of the Planck function is given by

B/ T = ( alpha

₁

₂

⁴/T²) · exp( alpha

₂

/T)/[exp(

₂

/T) - 1]²

Infrared approximation: for geq 600 cm^-1 and T leq 300 K.

(T)

₁

³ exp(-

₂

/T) mW · m^-2 · steradian^-1/cm^-1

T_b

₂ ·

)/ log_e [ ( alpha

₁

³/R

) ]

B/ T

(

₁

₂

⁴)/T² · exp[- alpha

₂

/T]

Microwave Rayleigh Jeans approximation: lambda (mm) = 300/f, = f/30 cm^-1, f is in GHz

Wavenumbers, , are frequency units and are assumed to be in vacuum while wavelength is the wavelength specified within the medium. Typically, wavelengths are expressed as wavelength in air, lambda _a or wavelength in vacuum, lambda _v.

10000/

_v = n_a · lambda

= 10000/(n_a · lambda

_a) n_a = 1.00027

f	cm^-1	µm	mm
0.66 GHz	0.02	454545	454.55	P band (SAR)
1.25 GHz	0.04	240000	240.00	C band (SAR)
5.33 GHz	0.18	56285	56.29	L band (SAR)
6.6 GHz	0.22	45454	45.45	MIMR (surface)
23 GHz	0.77	13043	13.04	AMSU-A
50 GHz	1.67	6000	6.00	AMSU-A
60 GHz	2.00	5000	5.00	AMSU-A
89 GHz	2.97	3371	3.37	AMSU-C
118 GHz	3.93	2542	2.54	MHS-X
183 GHz	6.10	1639	1.64	AMSU-B

₁/(

₂ · c² · 10^-18) · f² · T = 9.2105 · 10^-9 · f² · T mW · m^-2 · steradian^-1 ·/cm^-1

T_b

1.0857 · 10⁸ R

/f²

B/ T

2 · c · k ·

² =

₁/

₂ ·

² =

₁/(

₂ · c² · 10^-18) · f²

wavelength mm	frequency GHz	B(T=300K) mW/m²/ster/cm^-1	dB/dT mW/m²/ster/cm^-1/K	(1/B) · dB/dT %/K
6.0	50	0.007	0.000023	0.335
3.0	100	0.027	0.000092	0.336
2.0	150	0.061	0.000207	0.337
1.5	200	0.109	0.000368	0.338

wavelength µm	wavenumber cm^-1	B(T=300K) mW/m²/ster/cm^-1	dB/dT mW/m²/ster/cm^-1/K	(1/B) · dB/dT %/K
16.7	600	153.38	1.559	1.0
9.1	1100	81.49	1.441	1.8
6.2	1600	22.69	0.581	2.6
4.3	2300	2.35	0.086	3.7
3.7	2700	0.56	0.024	4.3
3.3	3000	0.18	0.009	4.8

Planetary Missions

Mars

1965

Mariner 4 : 22 low resolution pictures

1969

Mariner 6 : flyby

1969

Mariner 7 : flyby

1971

Mariner 9 : orbiter (resol. = .1-1 km)

1976

Vikings : 55,000 images, resol. 150-300 meters

Viking 1 orbiter (4 yrs)

Viking 1 lander 22.27N 47.97W

July 20, 1976 4:13 pm LMT

T=250 K

Viking 2 orbiter

Viking 2 lander 47.57N 225.74W

Sept. 3, 1976 9:49 am LMT

T=150 K diurnal variation 35-50K

Martian Year :

N. polar cap H₂O ice

S. polar cap CO₂ ice

Olympus Mons 600 km diameter volcano, 26 km tall

4 km high scarp (cliff) rings its base

``face'' on Mars is located in the Cydonia Mensae region at roughly 40.9 degrees North latitude and 9.45 degrees West longitude.

Outer Planet Mission Summary

Planet	Craft	Date	Julian	L_s
Jupiter	Pioneer 10	12/ 3/73	2442019.5	1.4
	Pioneer 11	12/ 2/74	2442383.5	33.9
	Voyager I	3/ 5/79	2443937.5	170.4
	Voyager II	7/ 9/79	2444063.5	180.4

Saturn	Pioneer 11	9/ 1/79	2444117.5	354.1
	Voyager I	11/12/80	2444555.5	8.9
	Voyager II	8/25/81	2444841.5	18.4

Uranus	Voyager II	1/24/86	2446454.5	271.3

Neptune	Voyager II	8/25/89	2447753.5	243.3

Potential Temperature

Derived directly from integration of the 1st law of thermodynamics. It is the temperature a parcel of air at P and T would have if it were at P_s. It is conserved for adiabatic motions, ( i.e., d Theta /dt = 0).

dQ/(n · <mw> · T) = (C_p dT/T) - (R_g dP/P) = 0

= T · (P_s/P) = P/( rho

R_g) [(P_s/P)] kappa

= R_g/C_p
For earth kappa

= 0.286 (<mw> = 28.96, C_p = 1.004 Joules/gram/K). Some authors write this equation with gamma

= C_p/C_v = 1/(1- kappa

)

P/ z = -

· g = (P · g)/(R_g · T) = - P/H(z)

log(P) = -H(z) · z
therefore,

P/P_s = e^{- dz'/H(z')}

= T · e^{- dz'/H(z')}
if H(z) = H₀

= T · e^{- · z/H₀}

Potential Vorticity

For adiabatic motion ( i.e., Theta is a constant) the density is rho = P^(C_v/C_p). For motions between layers of constant Theta

q = (

+ f) ·

/ p = constant
In the Shallow Water Model, where rho

is a constant ( i.e., incompressible), the conserved quantity is usually written as:

(

+ f)/(g h) seconds/meter²
example : flow over a mountain
<u> is eastward (westerly) then flow turns towards equator as it passes mountain, then oscillates around original latitude.
<u> is westward (easterly) then flow turns equatorward (note flow turning poleward `bucks' the flow causing it to turn equatorward. System is returned to original latitude after it passes mountain. No oscillations.

Radiative time constant

The volumetric heating rate, Q

Q/ T

Q_ir =

· T⁴ ·

/ z

_r = (

C_p)/(4

T³

/ z)
Harshvardan and Cess (1976, Tellus 28 p.1-10) give a value for Earth CO₂ of partial

/ z = -0.0081 per Km and Cess and Khetan (1973, JQSRT 13 p.995-1009) give a value for Jupiter, Saturn, Neptune, and Uranus of partial

/ z = -0.0068, -0.0063, -0.0061, and -0.0058 per Km, respectively.

_r = (

H C_p)/(4 epsilon

T³)
The phase shift, Phi

, is the seasonal lag due to the radiative time constant. It arises from the 1st Fourier moment of the thermal response. A value of Phi

=90° indicates a full seasonal shift ( e.g., the warm maximum expected at the summer solstice would occur at the autumnal equinox).

= tan^-1[ 2

_r/

_o ]
where tau

_o is the orbital period. For epsilon

= 0.3 the values are:

	T_eff K	P_eff mBar	gm/cm³	H Km	_rad years	phase °
Venus	229.0	20.000	4.6230e-05	4.862	0.007	3.94
Earth	255.0	500.000	6.8297e-04	7.471	0.131	39.47
Mars	210.0	6.000	1.5124e-05	10.605	0.006	1.17
Jupiter	124.0	400.000	8.6132e-05	19.146	4.534	67.39
Saturn	95.0	300.000	8.1128e-05	36.975	20.794	77.27
Uranus	59.0	430.000	2.0161e-04	24.234	131.311	84.15
Neptune	59.0	500.000	2.3443e-04	19.206	121.008	77.67
Titan	85.0	1.000	4.0568e-06	18.152	0.053	82.54

Radiative transfer Equation

_i,calc = B^-1

(R_i,calc)

R_i,calc = epsilon"

_i B_i(T_s) + rho

'_i H_i

'_i(p_s) cos( theta

₀) +

B_i(T(p)) (d tau

^u_i/dln p) (dln p) + rho

^u_i(p_s) integ

B_i(T(p)) (d tau

^d_i/dln p) (dln p)

B_i(T) is the Planck function evaluated at the effective channel wavenumber.
H_i is the channel averaged solar irradiance at the top of the atmosphere.
theta ₀ is the local zenith angle of the Sun.
tau '_i is the channel averaged two path transmittance from the Sun to the surface to the satellite.
tau ^u_i(p) is the atmospheric transmittance measured between p and the top of the atmosphere for channel i.
tau ^d_i(p) is the atmospheric transmittance between p and the surface for channel i.

Explicit retrieved parameters
epsilon _i is the surface emissivity at _i.
T_s is the surface temperature.
T(p) is the surface temperature profile.
rho _i is the surface spectral reflectivity at _i.
rho '_i is the surface spectral bidirectional reflectance of solar radiation at _i.

Implicit retrieved parameters ( i.e., within tau _i and tau '_i).
CO₂(p) is the carbon dioxide profile.
q(p) is the humidity (water) profile.
O₃(p) is the ozone profile.
CO(p) is the carbon monoxide profile.
CH₄(p) is the methane profile.
NO₂(p) is the nitrogen dioxide profile.

Rayleigh Scattering: Optical Depth

The average scattering cross section per particle is given by

(

) = (128

⁵

²)/(3

⁴) · [ (6 + 3 delta

)/(6 - 7

) ]

= (n - 1)/(2

N₀)

(n² - 1)/(4

N₀), for n near unity
where, n is the index of refraction, N₀ is the number of molecules per unit volume at standard temperature and pressure ( i.e., conditions of index of refraction), delta

is the depolarization factor.

The optical depth can be related to the ``thickness'' of the atmosphere. If Z is the thickness in Km-amagats then:

_ray(

) =

N(z) ·

(

) dz

(

) ·

N(z) · dz = Z · N₀ · sigma

(

)
The index of refraction has a wavelength dependence. This is usually represented by two constants, A and B, as follows:

(n-1) = A · (1 + B/ lambda

²),

in µm

(n-1)² = A² · (1 + 2 B/ lambda

² + B²/ lambda

⁴)

_ray = Z a₀/ lambda

⁴ · (1 + a₁/ lambda

² + a₂/

⁴) where,

a₀ = (32

³)/(3 N₀²) · [(6 + 3 delta

)/(6 - 7

) ] ·

q_i · A²

a₁ =

q_i · 2 B, and a₂ = sum

q_i · B²

_ray(H₂) = Z · 2.19 · 10^-4/ lambda

⁴ · ( 1 + 0.0157248/ lambda

² + 0.0001978/ lambda

⁴ ),

in µm
The wavelength dependence in the VIAMP code is taken from Dalgarno and Williams (ApJ, 1962). This equation is similar to the equation above, however, it differs in the lambda

⁸ term.

_ray(H₂) = (8.14 · 10^-13/ lambda

⁴ + 1.28 · 10^-6/ lambda

⁶ + 1.61/ lambda

⁸) cm²,

in Å
The optical depth per Km-amagat of hydrogen, denoted by tau

₁(H₂), is then

₁(H₂) = 2.687 · 10²⁴ · sigma

_ray(H₂) = 2.687 (8.14 · 10¹¹/ lambda

⁴ + 1.28 · 10¹⁸/ lambda

⁶ + 1.61 · 10²⁴/ lambda

⁸),

in Å

₁(H₂) = 2.687 (8.14 · 10^-21 f⁴ + 1.28 · 10^-30 f⁶ + 1.61 · 10^-40 f⁸), f = 10⁸/ lambda

and

in Å
And the total optical depth for a mixture of gases is given as

_ray =

₁(H₂) ·

Z_i · [ (n_i - 1)² / (n_H₂ - 1)² ]
Note that this formulation always uses the wavelength dependence of hydrogen, even if other gases are used.

(n-1) = A · (1 + B/ lambda

²),

in µm

ray = (n-1)²/(n_H₂ - 1)²

from Allen (pg. 92)
	ray	n	A (10^-5)	B (10^-3)	(10^-24)		a₀ µm⁴/Km
air	4.4459	1.0002918	28.71	5.67	3.40	0.031	10.7E-4
H₂	1.0000	1.0001384	13.58	7.52	1.61	0.02	2.35E-4
He	0.0641	1.0000350	3.48	2.30
O₂	3.8634	1.000272	26.63	5.07		0.054
N₂	4.6035	1.000297	29.06	7.7	3.44	0.030	10.9E-4
H₂O	3.3690	1.000254
CO₂	10.5611	1.0004498	43.9	6.4		0.09
CO	5.8247	1.000334	32.7	8.1
NH₃	7.3427	1.000375	37.0	12.0
NO	4.6035	1.000297	28.9	7.4
CH₄	10.1509	1.000441

The depth of penetration of Rayleigh scattering is computed for various objects using the data above. A summary of the characteristics of the plots in Figure 9 is given below (g is gravity in cm/s², µ = molecular weight in gm/mole, Z = KM-amagats per Bar).

Earth P₀ = 1013.25, g= 981, µ=28.97, Z=7.88
wave(µm):	0.1000	0.2000	0.2640	0.3000	0.4000	0.5000
(P₀):	209.57	6.95	2.05	1.19	0.36	0.14
P(=1):	4.8	145.7	493.2	851.0	2834.7	7094.5

Jupiter P₀ = 1000.00, g=2425.3, µ=2.22, Z=37.45/0.9
wave(µm):	0.1000	0.2000	0.2640	0.3000	0.4000	0.5000
(P₀):	299.82	8.62	2.47	1.42	0.42	0.17
P(=1):	3.3	116.1	405.2	706.3	2390.8	6030.4

Saturn P₀ = 1000.00, g= 1000, µ = 2.14, Z=100.5/0.96
wave(µm):	0.1000	0.2000	0.2640	0.3000	0.4000	0.5000
(P₀):	754.31	21.68	6.21	3.56	1.05	0.42
P(=1):	1.3	46.1	161.0	280.7	950.3	2396.9

Titan P₀ = 1500.00, g= 136, µ= 28.0, Z=58.85
wave(µm):	0.1000	0.2000	0.2640	0.3000	0.4000	0.5000
(P₀):	5378.65	152.59	43.58	24.98	7.37	2.92
P(=1):	0.3	9.8	34.4	60.1	203.6	513.9

The gas continuum absorption contains a term which is supposed to represent the effect of Raman scattering due to the ₁ vibration of H₂ at 4161 cm^-1.
Ref.: Belton et al. (1971). Atm. of Uranus. ApJ. 164, 191-209

_raman = 0.0208 · tau

_ray

Rayleigh Scattering: Phase Function

Definitions of Angles
See Figure 11. The angle between the incident flux and the local normal is given by alpha and µ₀ ident cos( alpha ). The angle between the local normal and the observer is given by epsilon and µ ident cos( epsilon ). The phase angle, theta , is the angle between the incident and emission through the origin. The azimuthal angle, Delta psi , is the projection of the solar incidence and emission directions onto the local horizon. Using spherical trigonometry cosine laws (e.g., see CRC pg. 146) we can easily obtain the value of Delta psi ) given µ₀, µ, and theta . For solar scattering to an observer above the atmosphere the angles are related by:

cos(

) =

[(1-µ₀²)(1-µ²)] · cos( Delta

) -/+ µ µ₀ (S = +, T = -)

This is the method employed by Chandrasekar, Liou, and others. We could also write the equations in terms of the scattering angles. The scattering angle between incidence and emission, Theta , which is related to the phase function, is given by Theta = - theta . The scattering angle in the horizontal plane, Delta phi is related to the azimuthal angle, and is given by Delta phi = - Delta psi . This definition is used by Hansen, Tomasko, and Danielson. It is the method employed within the VIAMP programs. Note the sign change between the two methods.

cos(

) =

[ (1-µ₀²)(1-µ²)] · cos( Delta

) ± µ µ₀ (T = +, S = -)

The Rayleigh phase function is given in terms of scattering angles or phase angles by

P_ray(

) = (3/4) (1 + cos²( Theta

)) = (3/4)(1 + cos²( theta

)) = P_ray( theta

)
The cos² term can be expressed in terms of µ, µ₀, and Delta

cos²(

) = (1-µ₀²)(1-µ²) · cos²( Delta

) ± 2µµ₀ sqrt

[ (1-µ₀²)(1-µ²) ] · cos( Delta

) + (µ² µ₀²)

cos(2

) = 2 cos²( phi

) - 1 or,

cos²(

) = 1/2 cos(2 Delta

) + 1/2

cos²(

) = 1/2 (1-µ₀²)(1-µ²) · cos(2 Delta

) ± 2 µ µ₀ sqrt

[ (1-µ₀²)(1-µ²) ] · cos( Delta

) + µ² µ₀² + 1/2 (1-µ₀²)(1-µ²)

So the Rayleigh phase function can be written in terms of 3 Fourier moments:

P_ray(

) = P₁ + P₂ cos( Delta

) + P₃ cos(2 Delta

)
where the 3 coefficients are equal to

P₀ = 3/4 [ 1 + µ² µ₀² + 1/2 (1-µ₀²)(1-µ²) ] = 3/8 ( 3 + 3 µ² µ₀² -µ₀² -µ² )

P₁ = ± 3/2 ( µ µ₀ sqrt

[(1-µ₀²)(1-µ²)] ) (T = +, S = -)

P₂ = 3/8 (1-µ₀²)(1-µ²)

Richardson Number

Dynamically significant stability indicator (similar to Burger number). As Ri --> 0 convection becomes strong.

Ri/Ro = Effect of vertical motions / Effect of Non-linear terms
when the Rossby Number, Ro geq

1 then the static stability buoyancy frequency, N = Ri/Ro. When Ro

1, N = Bo/Ro

Ri = (g · d Theta

/dz)/ [T₀ · (dU/dz)²] = N²/(dU/dz)²
Stone 1972 JAS 29 p. 405. For Jupiter: d Theta

/dz = 6.0 · 10^-10 K/cm and du/dz = 3.8 · 10^-4 cm/s, then Ri = 3.7 · 10^-3

Rossby Number

A small Rossby number indicates that the geostrophic approximation is valid ( i.e., du/dt = dv/dt = 0) and that the Coriolis acceleration, v · f, is greater than the horizontal fluid acceleration, du/dt.

Ro = (du/dt)/(v f) approx

(v²/r)/(v f) = (v/r)/f = U/(f₀ · L)
For the GRS, hurricanes, etc.

Ro = (V_t a/b²/ eta

³)/f

² = [ cos²( theta

) + (a⁴/b⁴) · sin²( theta

) ] / [ cos²( theta

) + (a²/b²) · sin²( theta

) ]
where V_t is the tangential velocity, a is the semimajor axis, b is the semiminor axis, and theta

is the angle between the semi-major axis and the direction of motion. Mitchell et al. 1981 JGR 86 p.8751.

	terrestrial	Red Spot	FA/BC/DE	small spots
V_t		110 m/s	120 m/s
a		1.1E7 m	4.9E6 m
Ro(0)		.36	.36
Ro(90)		.04	.08
g.lat		22 S	33 S	40.5 S

Great Red Spot

40000 x 13000 km (1879-1882)

20-60 m/s velocity around spot, 6 day period

bounded by Jets at -19.5 (-60 m/s) and -27.0 (+50 m/s) graphic latitude

long drift = -3.4 m/s

± 1/2 degree longitude oscillation with 90 day period

anticyclonic (counterclockwise in southern hemisphere)

Saturation Vapor Pressure

Given T in Kelvin these equations will give e_s in milliBar.
from Fleagle and Businger, Vol.5, pg. 62 (QC880.F59)
The first law can be written as

L = T · (S₂-S₁) = U₂ - U₁ + P_s · ( alpha

₂ -

₁)
where alpha

₁

₁ and index 1 refers to the liquid phase and index 2 refers to the gas phase.

For an isothermal change of phase, the Clausius-Clapeyron equation has the form

d P_s/d T = L/[T · ( alpha

₂-

₁)]
Water vapor behaves like an ideal gas and alpha

₂

₁ for a change in state.

2.5 · 10³ Joules/gm

2.824 · 10³ Joules/gm over ice

R_w = R_*/<mw>_w = 8.3143/18.016 = 0.4615 Joules/gm/K

P_s =

₂ · R_w T

d P_s/d T = L/[T · ( alpha

₂-

₁)]

(L ·

₂)/T = (L · P_s) /(R_w · T²)

d log(e_s) = d P_s/P_s = (L/R_w) · (dT/T²)

log_e(e_s) = integ

(L/R_w) · (dT/T²) = -(L/R_w)|T->T₀ + C = -L/(R_w · T₀) + L/(R_w· T) + C
at triple point all 3 phases can exist in equilibrium, 0.0098° C and P_s = 6.11 mB

e_s(T=T₀) = 6.11

L/R_w = 5417.12

L/(R_w T₀) = 19.8313

6.11 · exp[ L/(R_w T₀) ] = 2.504 · 10⁹

e_s(T) = 6.11 · exp[ 5417( 1/T₀ - 1/T) ] = 2.504 · 10⁹ · exp[ 5417/T ]

Undocumented fit is used in the program watsat.F (over liquid)

e_s = 2.229 · 10⁹ · exp[ -5385/T ]
Note this is the same equation as above, except that it assumes L = 2485.2 Joules/gm and T₀ = 273.15 ° K
Another undocumented fit is given (but not used) in the program watsat.F

e_s = 0.001 · exp[ a/T + b + c log(T) + d · T + e · T² ]

coef	over ice	over water
a	-5631.1206	-2313.0338
b	-8.363602	-164.03307
c	8.2312	38.053682
d	-3.861449 · 10^-2	-1.3844344 · 10^-1
e	2.77494 · 10^-5	7.4465367 · 10^-5

From Rogers and Yau, pg. 16

e_s = 6.112 · exp[ a · (T-273.16)/(T-b) ]

coef	Rogers & Yau over water
a	17.67
b	29.66

Murray, F.W. 1966. ``On the computation of Saturation Vapor Pressure'' J. Appl. Meteor. 6 p.204

e_s = 6.1078 · exp[ a · (T-273.16)/ (T-b) ]

coef	Murray over ice	Murray over water
a	21.8745584	17.2693882
b	7.66	35.86

Saucier, W.J. 1883. ``Principles of Meteorological Analysis'' Dover pg. 9 who uses values of Tetens (1930). Note, he used 10^{[(a'T)/(T-b')]} with T in Centigrade so to convert into the form above a = log 10 · a' and b = 273.16-b'.

coef	over ice	over water
a	21.875	17.27
b	7.66	35.86

Thermal Wind Equation

Relationship between meridional temperature gradient and vertical wind shear due to non-uniform horizontal heating. Note: dy = R_e · d phi . Hydrostatic and geostrophic balance yields:

U_g/ P = (1/f) partial

/ y (1/ rho

) = R_g/(f · P) (dT/dy)

U(z₂) = U(z₁) - (R/f) · dT/dy|_P · log(P₁/P₂)

f₀ dU/dz = (R_g/H) (dT/dy)

Velocity of sound

dU/dt + 1/ rho

(

/ x) = 0

/dt +

( U/ x) = 0

d log(

)/dt = 0

V_s =

[

R_g T ], gamma

= C_p/C_v

Vorticity

Relative vorticity tend to be conserved in storm systems.

= k · × V = dv/dx - du/dy

Absolute vorticity tends to be conserved following the motion ( i.e., forecasting).

+ f = k · × V_a

If eta is positive then it is cyclonic and if eta is negative then anti-cyclonic.

Weighting Functions

The outgoing radiance or upward radiance, R^u, for channel i from an atmospheric column is given by

R_i^u =

B_i(T(p)) · ( partial

^u(p)/

ln p) d ln p
The weighting function is defined as

W(p)

^u(p)/

ln p
and the contribution function is the integrand of the outgoing radiance calculation

C(p)

B_i(T(p)) · ( partial

^u(p)/

ln p)
and can be normalized as

C(p)

B_i(T(p))/R_i^u · ( partial

^u(p)/

ln p)
the information content will require derivative w.r.t. temperature of the radiation transfer equation and, therefore, the Kernel function represents the best estimate of the sounding level for temperature retrievals.

K(p)

( B_i(T(p))/ T) · ( partial

^u(p)/

ln p)

Wind Measurement

The meridional velocity is the distance, r · Delta theta , divided by the time difference, Delta t. Since the radius is given in Km's and the time is given in hours we need factors of 1000 and 3600, respectively, to convert to meters per second. If theta is given in degrees then:

V = 1000 R( theta

) · (

/180)(

₁ -

₀)/(3600

t)
To calculate the zonal velocity we need to calculate the displacement along a latitude circle, (i.e., Delta

/ 360), during the time interval Delta

(t₁) -

(t₀)

U = 2

R(<

>) cos(< theta

>) · (1000/3600) · Delta

/(360

t)
Alternatively, we can calculate the period of rotation of the measured feature, P, and define the wind relative to the system of measure, P_ref as follows:

P = 360

t/[

+ (360

t/P_ref) ]
so that,

U = 2

R(<

>) cos(< theta

>) · (1000/3600) · ( 1/P - 1/P_ref )

Encyclopedia Author-Chris Barnet
HTML Editor-Steve Duran
Please E-mail Lyle Huber for any comments or suggestions.
Thank You.

Menu: Skip within this page

Menu: Help Links

Main menu

Home submenu

Quick Searches by Target

PDS Nodes

PDS Support

Data Analysis Proposals Support

Welcome to the PDS Atmospheres Node

Standard Planetary Information, Formulae and Constants

TABLE OF CONTENTS

Earth Constants

Unit Conversion

Cloud clearing, N* method

Forward Cosine transform

Inverse Cosine Transform

Absolute humidity

Specific humidity

Mass Mixing Ratio

% Relative Humidity

Dew Point Temperature

Jupiter

Saturn

Orbits: Earth

Mars

Outer Planet Mission Summary

Cloud clearing, N^* method